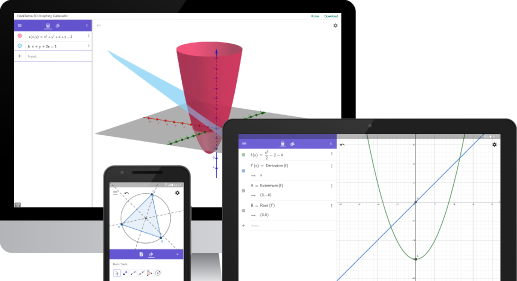
Leibniz
O matemático e filósofo alemão Gottfried Wilhelm von Leibniz, nasceu em 1º de julho de 1646, e morreu em 14 de novembro de 1716. Foi um gênio universal e um fundador de ciência moderna. Ele antecipou o desenvolvimento de LÓGICA simbólica e, independentemente de Isaac Newton, inventou o cálculo com uma notação superior, incluindo os símbolos para integração e diferenciação. Leibniz também defendeu ecumenismo Cristão na religião, leis romanas codificadas e lei natural em jurisprudência, propôs a lei metafísica de otimismo (satirizada por Voltaire em Candide) que nosso universo é o "melhor de todos os possíveis mundos", e transmitiu o pensamento chinês para a Europa. Para o seu trabalho, ele é considerado um progenitor de idealismo alemão e um pioneiro do Esclarecimento.
Leibniz era o filho de um professor de filosofia moral em Leipzig. Uma juventude precoce, Leibniz aprendeu sozinho o latim e algum grego aos 12 anos de idade, podendo então ler os livros na biblioteca de seu pai. De 1661 a 1666 ele esteve na Universidade de Leipzig. Quando recusou admissão a seu programa doutoral em lei de 1666, ele foi para a Universidade de Altdorf que lhe premiou com o doutorado em jurisprudência em 1667. Na tradição de Cícero e Francis Bacon, Leibniz escolheu procurar a vida ativa de um cortesão. Ele recusou um cargo de professor a Altdorf porque ele tinha "coisas muito diferentes à vista". Depois de servir como secretário da Sociedade de Rosicrucian em Nuremberg em 1667, ele se mudou para Frankfurt para trabalhar em reforma legal. De 1668 a 1673 ele serviu o eleitor-arcebispo de Mainz. Lhe enviaram para Paris em 1672 para tentar dissuadir Louis XIV de atacar áreas alemãs. Leibniz propôs uma campanha contra o Egito e também para construir um canal pelo Istmo de Suez. Embora suas propostas fossem despercebidas, Leibniz permaneceu até 1676 em Paris, onde ele praticou leis, examinou pensamento Cartesiano com Nicolas Malebranche e Antoine Arnauld, e estudou Matemática e Física com Christian Huygens.
De 1676 até a sua morte, Leibniz serviu a família de Brunswick em Hanover como bibliotecário, juiz e ministro. Depois de 1686 ele serviu principalmente como historiador, preparando uma genealogia dos Hanovers baseada no exame crítico de materiais de fonte primária. À procura de fontes, ele viajou para a Áustria e Itália de 1687 a 1690. Por causa de seu fundo luterano, ele recusou a posição de guarda da Biblioteca Vaticana que requeria a conversão dele ao Catolicismo.
Nos seus últimos anos, Leibniz tentou construir uma armação institucional para as ciências na Europa central e Rússia. Ao urgir dele, a Sociedade de Brandenburg (Academia de Ciência de Berlim) foi fundado em 1700. Ele encontrou-se várias vezes com Peter o Grande para recomendar reformas educacionais na Rússia e propôs o que depois se tornou a Academia de Ciência de Saint Petersburg.
Embora tímido e livresco, Leibniz não conheceu nenhum mestre em disputa. Depois de 1700 ele opôs a teoria de John Locke que a mente é uma tabula rasa (tablete em branco) no nascimento e que nós só aprendemos pelos juízos. Ele protestou fortemente a carga da Sociedade Real (1712-13) de plágio contra ele relativo à invenção do cálculo. No debate final dele com Samuel Clarke, que defendeu ciência Newtoniana, Leibniz discutiu que espaço, tempo e movimento são relativos.
Os trabalhos mais importante de Leibniz são: o de Essais Theodicee (1710) em que muito de sua filosofia geral é achada, e o Monadology (1714). O trabalho dele foi sistematizado e foi modificado no século 18 pelo filósofo alemão Christian Wolff.
Leibniz era o filho de um professor de filosofia moral em Leipzig. Uma juventude precoce, Leibniz aprendeu sozinho o latim e algum grego aos 12 anos de idade, podendo então ler os livros na biblioteca de seu pai. De 1661 a 1666 ele esteve na Universidade de Leipzig. Quando recusou admissão a seu programa doutoral em lei de 1666, ele foi para a Universidade de Altdorf que lhe premiou com o doutorado em jurisprudência em 1667. Na tradição de Cícero e Francis Bacon, Leibniz escolheu procurar a vida ativa de um cortesão. Ele recusou um cargo de professor a Altdorf porque ele tinha "coisas muito diferentes à vista". Depois de servir como secretário da Sociedade de Rosicrucian em Nuremberg em 1667, ele se mudou para Frankfurt para trabalhar em reforma legal. De 1668 a 1673 ele serviu o eleitor-arcebispo de Mainz. Lhe enviaram para Paris em 1672 para tentar dissuadir Louis XIV de atacar áreas alemãs. Leibniz propôs uma campanha contra o Egito e também para construir um canal pelo Istmo de Suez. Embora suas propostas fossem despercebidas, Leibniz permaneceu até 1676 em Paris, onde ele praticou leis, examinou pensamento Cartesiano com Nicolas Malebranche e Antoine Arnauld, e estudou Matemática e Física com Christian Huygens.
De 1676 até a sua morte, Leibniz serviu a família de Brunswick em Hanover como bibliotecário, juiz e ministro. Depois de 1686 ele serviu principalmente como historiador, preparando uma genealogia dos Hanovers baseada no exame crítico de materiais de fonte primária. À procura de fontes, ele viajou para a Áustria e Itália de 1687 a 1690. Por causa de seu fundo luterano, ele recusou a posição de guarda da Biblioteca Vaticana que requeria a conversão dele ao Catolicismo.
Nos seus últimos anos, Leibniz tentou construir uma armação institucional para as ciências na Europa central e Rússia. Ao urgir dele, a Sociedade de Brandenburg (Academia de Ciência de Berlim) foi fundado em 1700. Ele encontrou-se várias vezes com Peter o Grande para recomendar reformas educacionais na Rússia e propôs o que depois se tornou a Academia de Ciência de Saint Petersburg.
Embora tímido e livresco, Leibniz não conheceu nenhum mestre em disputa. Depois de 1700 ele opôs a teoria de John Locke que a mente é uma tabula rasa (tablete em branco) no nascimento e que nós só aprendemos pelos juízos. Ele protestou fortemente a carga da Sociedade Real (1712-13) de plágio contra ele relativo à invenção do cálculo. No debate final dele com Samuel Clarke, que defendeu ciência Newtoniana, Leibniz discutiu que espaço, tempo e movimento são relativos.
Os trabalhos mais importante de Leibniz são: o de Essais Theodicee (1710) em que muito de sua filosofia geral é achada, e o Monadology (1714). O trabalho dele foi sistematizado e foi modificado no século 18 pelo filósofo alemão Christian Wolff.